第一节：1D数学

1.基本数学概念

• 自然数：人类在大自然中对自己的羊或者牛进行计数，而出现自然数，所以从0到N的整数被称为自然数。
• 负数：有时候人类在交易物品的时候会先赊着，此时就是用负数表示。
• 分数：人类在交易物品的时候，例如卖羊的时候，我们可能吃不了那么多，只需要1/4的羊肉，此时就产生了分数。
• 无理数：人类文明在进化的过程中，需要用到一些特殊的数，例如π，这种无限不循环小数被称为无理数。

2.基本数学概念的图示

      

3.离散数学和连续数学

• 研究自然数和整数的领域称作离散数学，研究实数领域称作连续数学。
• 所谓的离散就是可数的，例如我数地球上的所有物体的个数，仅用离散数学就可以做到，并且只需要一个很大的自然数就可以完成。
• 连续数学是不可数的，例如外星文明，它们从来不是呀π，而是使用3.1415926....，这样的文明用这样的准确数字就可以建造更完美的世界。

4.C++中提供的数据类型

• C++中提供的都是有理数，short，int是整数，float，double是分数或者叫小数。

第二节：2D数学

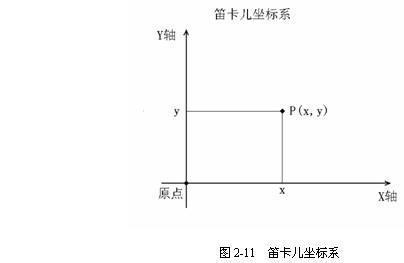
1.笛卡尔坐标系

　　所谓的笛卡尔坐标系就是两条相互垂直的数轴组成的一个平面，笛卡尔坐标系有两两条轴x和y轴。我们可以标记这个平面上的任意一个点。

　　

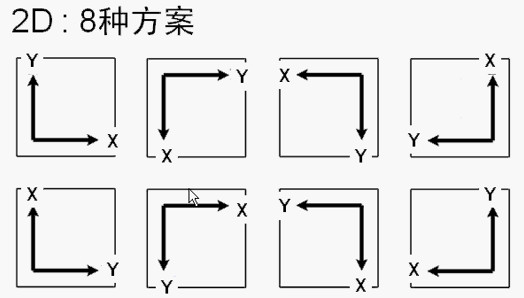
2.笛卡尔坐标有8种方案

     

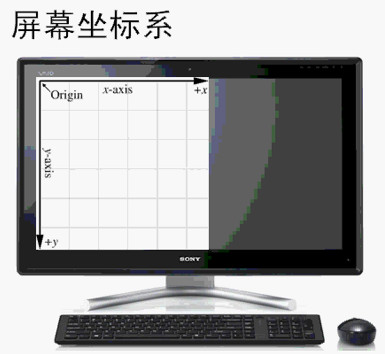
　　常见的屏幕坐标系就是上述图中的第6种方案，而我们平常的书写方式是第一种方案。

　　

第三节：3D数学

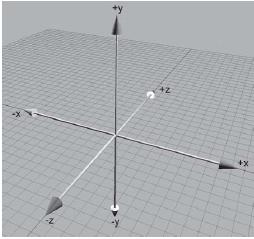
1.3D坐标系

　　3D坐标系就是在笛卡尔坐标系的基础上添加了z轴，于是就形成了三个面，xy面，xz面和yz面，这三个面互相垂直构成一个立体的空间。

　　

2.左手坐标系和右手坐标系

　　3D坐标系可以有多种构成方式，不过通过结论可以得知所有的3D坐标系无非两种坐标系即左手和右手坐标系，其他的坐标系可以通过左手右手坐标系进行旋转得到。

　　

　　第一幅图是左手坐标系，第二幅图是右手坐标系。

　　通常我们是选用左手坐标系，例如著名的建模软件3DMax缺省方向是+x向右，+y向前，+z向上。通过我们用左手和右手坐标系进行旋转可以发现是左手坐标系，而右手坐标系是无法通过旋转得到的。

　　左手坐标系常见的有：DirectX,3DMax

　　右手坐标系常见的有：OpenGL

3.3D坐标系有48中组合方案

　　这48种方案中，有24种是左手坐标系（即可以通过左手坐标系旋转而得到），另外的24种是右手坐标系（即可以通过右手坐标系旋转而得到）。